BY NICK MCCREA – SOFTWARE ENGINEER @ TOPTAL. (Original article posted here)
Let’s face it, robots are cool. They’re also going to run the world someday, and hopefully at that time they will take pity on their poor soft fleshy creators (AKA robotics developers) and help us build a space utopia filled with plenty. I’m joking of course, but only sort of.
In my ambition to have some small influence over the matter, I took a course in autonomous robot control theory last year, which culminated in my building a simulator that allowed me to practice control theory on a simple mobile robot.
In this article, I’m going to describe the control scheme of my simulated robot, illustrate how it interacts with its environment and achieves its goals, and discuss some of the fundamental challenges of robotics programming that I encountered along the way.
The Challenge of the Robot: Perception vs. Reality and the Fragility of Control
The fundamental challenge of all robotics is this: It is impossible to ever know the true state of the environment. A robot can only guess the state of the real world based on measurements returned by its sensors. It can only attempt to change the state of the real world through the application of its control signals.
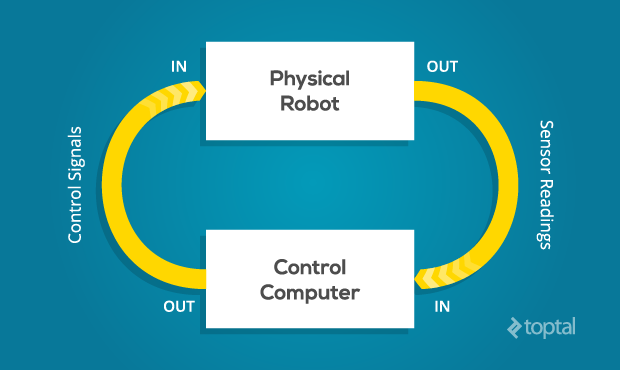
A robot can only guess the state of the real world based on measurements returned by its sensors.
Thus, one of the first steps in control design is to come up with an abstraction of the real world, known as a model, with which to interpret our sensor readings and make decisions. As long as the real world behaves according to the assumptions of the model, we can make good guesses and exert control. As soon as the real world deviates from these assumptions, however, we will no longer be able to make good guesses, and control will be lost. Often, control once lost can never be regained. (Unless some benevolent outside force restores it.)
This is one of the key reasons that robotics programming is so difficult. We often see video of the latest research robot in the lab, performing fantastic feats of dexterity, navigation, or teamwork, and we are tempted to ask, “Why isn’t this used in the real world?” Well, next time you see such a video, take a look at how highly-controlled the lab environment is. In most cases, these robots are only able to perform these impressive tasks as long as the environmental conditions remain within the narrow confines of its internal model. Thus, a key to the advancement of robotics is the development of more complex, flexible, and robust models – advancement which is subject to the limits of the available computational resources.
A key to the advancement of robotics is the development of more complex, flexible, and robust models.
[Side Note: Philosophers and psychologists alike would note that living creatures also suffer from dependence on their own internal perception of what their senses are telling them. Many advances in robotics come from observing living creatures, and seeing how they react to unexpected stimuli. Think about it. What is your internal model of the world? It is different from that of an ant, and that of a fish (hopefully). However, like the ant and the fish, it is likely to oversimplify some realities of the world. When your assumptions about the world are not correct, it can put you at risk of losing control of things. Sometimes we call this “danger.” The same way our little robot struggles to survive against the unknown universe, so do we all. This is a powerful insight for roboticists.]
The Robot Simulator
The simulator I built is written in Python and very cleverly dubbed Sobot Rimulator. You can find v1.0.0 here on GitHub. It does not have a lot of bells and whistles but it is built to do one thing very well: provide an accurate simulation of a robot and give an aspiring roboticist an interface for practicing control robot programming. While it is always better to have a real robot to play with, a good robot simulator is much more accessible, and is a great place to start.
The software simulates a real life research robot called the Khepera III. In theory, the control logic can be loaded into a real Khepera III robot with minimal refactoring, and it will perform the same as the simulated robot. In other words, programming the simulated robot is analogous to programming the real robot. This is critical if the simulator is to be of any use.
In this tutorial, I will be describing the robot control architecture that comes with v1.0.0 of Sobot Rimulator, and providing snippets from the source (with slight modifications for clarity). However I encourage you to dive into the source and mess around. Likewise, please feel free to fork the project and improve it.
The control logic of the robot is constrained to these files:
models/supervisor.pymodels/supervisor_state_machine.py- the files in the
models/controllersdirectory
The Robot
Every robot comes with different capabilities and control concerns. Let’s get familiar with our simulated robot.
The first thing to note is that, in this guide, our robot will be an autonomous mobile robot. This means that it will move around in space freely, and that it will do so under its own control. This is in contrast to, say, an RC robot (which is not autonomous) or a factory robot arm (which is not mobile). Our robot must figure out for itself how to achieve it’s goals and survive in its environment, which proves to be a surprisingly difficult challenge for a novice robotics programmer.
Control Inputs – Sensors
There are many different ways a robot may be equipped to monitor its environment. These can include anything from proximity sensors, light sensors, bumpers, cameras, and so forth. In addition, robots may communicate with external sensors that give it information the robot itself cannot directly observe.
Our robot is equipped with 9 infrared proximity sensors arranged in a “skirt” in every direction. There are more sensors facing the front of the robot than the back, because it is usually more important for the robot to know what is in front of it than what is behind it.
In addition to the proximity sensors, the robot has a pair of wheel tickers that track how many rotations each wheel has made. One full forward turn of a wheel counts off 2765 ticks. Turns in the opposite direction count backwards.
Control Outputs – Mobility
Some robots move around on legs. Some roll like a ball. Some even slither like a snake.
Our robot is a differential drive robot, meaning that it rolls around on two wheels. When both wheels turn at the same speed, the robot moves in a straight line. When the wheels move at different speeds, the robot turns. Thus, controlling movement of this robot comes down to properly controlling the rates at which each of these two wheels turn.
API
In Sobot Rimulator, the separation between the robot “computer” and the (simulated) physical world is embodied by the file robot_supervisor_interface.py, which defines the entire API for interacting with the “real world” as such:
read_proximity_sensors()returns an array of 9 values in the sensors’ native formatread_wheel_encoders()returns an array of 2 values indicating total ticks since startset_wheel_drive_rates( v_l, v_r )takes two values, in radians-per-second
The Goal
Robots, like people, need purpose in life. The goal of programming this robot will be very simple: it will attempt to make its way to a predetermined goal point. The coordinates of the goal are programmed into the control software before the robot is activated.
However, to complicate matters, the environment of the robot may be strewn with obstacles. The robot MAY NOT collide with an obstacle on its way to the goal. Therefore, if the robot encounters an obstacle, it will have to find its way around so that it can continue on its way to the goal.
A Simple Model
First, our robot will have a very simple model. It will make many assumptions about the world. Some of the important ones include:
- the terrain is always flat and even
- obstacles are never round
- the wheels never slip
- nothing is ever going to push the robot around
- the sensors never fail or give false readings
- the wheels always turn when they are told to
The Control Loop
A robot is a dynamic system. The state of the robot, the readings of its sensors, and the effects of its control signals, are in constant flux. Controlling the way events play out involves the following three steps:
- Apply control signals.
- Measure the results.
- Generate new control signals calculated to bring us closer to our goal.
These steps are repeated over and over until we have achieved our goal. The more times we can do this per second, the finer control we will have over the system. (The Sobot Rimulator robot repeats these steps 20 times per second, but many robots must do this thousands or millions of times per second in order to have adequate control.)
In general, each time our robot takes measurements with its sensors, it uses these measurements to update its internal estimate of the state of the world. It compares this state to a reference value of what it wants the state to be, and calculates the error between the desired state and the actual state. Once this information is known, generating new control signals can be reduced to a problem of minimizing the error.
A Nifty Trick – Simplifying the Model
To control the robot we want to program, we have to send a signal to the left wheel telling it how fast to turn, and a separate signal to the right wheel telling it how fast to turn. Let’s call these signals vL and vR. However, constantly thinking in terms of vL and vR is very cumbersome. Instead of asking, “How fast do we want the left wheel to turn, and how fast do we want the right wheel to turn?” it is more natural to ask, “How fast do we want the robot to move forward, and how fast do we want it to turn, or change its heading?” Let’s call these parameters velocity v and angular velocity ω (a.k.a. omega). It turns out we can base our entire model on v and ω instead of vL and vR, and only once we have determined how we want our programmed robot to move, mathematically transform these two values into vL and vR with which to control the robot. This is known as a unicycle model of control.

Here is the code that implements the final transformation in supervisor.py. Note that if ω is 0, both wheels will turn at the same speed:
# generate and send the correct commands to the robot
def _send_robot_commands( self ):
...
v_l, v_r = self._uni_to_diff( v, omega )
self.robot.set_wheel_drive_rates( v_l, v_r )
def _uni_to_diff( self, v, omega ):
# v = translational velocity (m/s)
# omega = angular velocity (rad/s)
R = self.robot_wheel_radius
L = self.robot_wheel_base_length
v_l = ( (2.0 * v) - (omega*L) ) / (2.0 * R)
v_r = ( (2.0 * v) + (omega*L) ) / (2.0 * R)
return v_l, v_r
Estimating State – Robot, Know Thyself
Using its sensors, the robot must try estimate the state of the environment as well as its own state. These estimates will never be perfect, but they must be fairly good, because the robot will be basing all of its decisions on these estimations. Using its proximity sensors and wheel tickers alone, it must try to guess the following:
- the direction to obstacles
- the distance from obstacles
- the position of the robot
- the heading of the robot
The first two properties are determined by the proximity sensor readings, and are fairly straightforward. The API function read_proximity_sensors() returns an array of nine values, one for each sensor. We know ahead of time that the seventh reading, for example, corresponds to the sensor that points 75 degrees to the right of the robot. Thus, if this value shows a reading corresponding to 0.1 meters distance, we know that there is an obstacle 0.1 meters away, 75 degrees to the left. If there is no obstacle, the sensor will return a reading of its maximum range of 0.2 meters. Thus, if we read 0.2 meters on sensor seven, we will assume that there is actually no obstacle in that direction.
Because of the way the infrared sensors work (measuring infrared reflection), the numbers they return are are a non-linear transformation of the actual distance detected. Thus, the code for determining the distance indicated must convert these readings into meters. This is done in supervisor.py as follows:
# update the distances indicated by the proximity sensors
def _update_proximity_sensor_distances( self ):
self.proximity_sensor_distances = [ 0.02-( log(readval/3960.0) )/30.0 for
readval in self.robot.read_proximity_sensors() ]
Determining the position and heading of the robot (together, known as the pose in robotics programming), is somewhat more challenging. Our robot uses odometry to estimate its pose. This is where the wheel tickers come in. By measuring how much each wheel has turned since the last iteration of the control loop, it is possible to get a good estimate of how the robot’s pose has changed – but only if the change is small. This is one reason it is important to iterate the control loop very frequently. If we waited too long to measure the wheel tickers, both wheels could have done quite a lot, and it will be impossible to estimate where we have ended up.
Below is the full odometry function in supervisor.py that updates the robot pose estimation. Note that the robot’s pose is composed of the coordinates x and y, and the heading theta, which is measured in radians from the positive x-axis. Positive x is to the east and positive y is to the north. Thus a heading of 0 indicates that the robot is facing directly east. The robot always assumes its initial pose is (0, 0), 0.
# update the estimated position of the robot using it's wheel encoder readings
def _update_odometry( self ):
R = self.robot_wheel_radius
N = float( self.wheel_encoder_ticks_per_revolution )
# read the wheel encoder values
ticks_left, ticks_right = self.robot.read_wheel_encoders()
# get the difference in ticks since the last iteration
d_ticks_left = ticks_left - self.prev_ticks_left
d_ticks_right = ticks_right - self.prev_ticks_right
# estimate the wheel movements
d_left_wheel = 2*pi*R*( d_ticks_left / N )
d_right_wheel = 2*pi*R*( d_ticks_right / N )
d_center = 0.5 * ( d_left_wheel + d_right_wheel )
# calculate the new pose
prev_x, prev_y, prev_theta = self.estimated_pose.scalar_unpack()
new_x = prev_x + ( d_center * cos( prev_theta ) )
new_y = prev_y + ( d_center * sin( prev_theta ) )
new_theta = prev_theta + ( ( d_right_wheel - d_left_wheel ) / self.robot_wheel_base_length )
# update the pose estimate with the new values
self.estimated_pose.scalar_update( new_x, new_y, new_theta )
# save the current tick count for the next iteration
self.prev_ticks_left = ticks_left
self.prev_ticks_right = ticks_right
Now that our robot is able to generate a good estimate of the real world, let’s use this information to achieve our goals.
Related: Video Game Physics Tutorial – Collision Detection for Solid Objects
Go-to-Goal Behavior
The supreme purpose in our little robot’s existence in this programming tutorial is to get to the goal point. So how do we make the wheels turn to get it there? Let’s start by simplifying our worldview a little and assume there are no obstacles in the way.
This then becomes a simple task. If we go forward while facing the goal, we will get there. Thanks to our odometry, we know what our current coordinates and heading are. We also know what the coordinates of the goal are, because they were pre-programmed. Therefore, using a little linear algebra, we can determine the vector from our location to the goal, as in go_to_goal_controller.py:
# return a go-to-goal heading vector in the robot's reference frame
def calculate_gtg_heading_vector( self ):
# get the inverse of the robot's pose
robot_inv_pos, robot_inv_theta = self.supervisor.estimated_pose().inverse().vector_unpack()
# calculate the goal vector in the robot's reference frame
goal = self.supervisor.goal()
goal = linalg.rotate_and_translate_vector( goal, robot_inv_theta, robot_inv_pos )
return goal
Note that we are getting the vector to the goal in the robot’s reference frame, and NOT in the world coordinates. If the goal is on the x-axis in the robot’s reference frame, that means it is directly in front of the robot. Thus, the angle of this vector from the x-axis is the difference between our heading and the heading we want to be on. In other words, it is the error between our current state and what we want our current state to be. We therefore want to adjust our turning rate ω so that the angle between our heading and the goal will change towards 0. We want to minimize the error.
# calculate the error terms
theta_d = atan2( self.gtg_heading_vector[1], self.gtg_heading_vector[0] )
# calculate angular velocity
omega = self.kP * theta_d
self.kP in the above code is a control gain. It is a coefficient which determines how fast we turn in proportion to how far away from the goal we are facing. If the error in our heading is 0, then the turning rate is also 0.
Now that we have our angular velocity ω, how do we determine forward velocity v? A good general rule of thumb is one you probably know instinctively: if we are not making a turn, we can go forward at full speed, but the faster we are turning, the more we should slow down. This generally helps us keep our system stable and acting within the bounds of our model. Thus, v is a function of ω. In go_to_goal_controller.py the equation is:
# calculate translational velocity
# velocity is v_max when omega is 0,
# drops rapidly to zero as |omega| rises
v = self.supervisor.v_max() / ( abs( omega ) + 1 )**0.5
OK, we have almost completed a single control loop. The only thing left to do is transform these two unicycle-model parameters into differential wheel speeds, and send the signals to the wheels. Here’s an example of the robot’s trajectory under the Go-to-Goal controller, with no obstacles:

As we can see, the vector to the goal is an effective reference for us to base our control calculations on. It is an internal representation of “where we want to go.” As we will see, the only major difference between Go-to-Goal and other behaviors is that sometimes going towards the goal is a bad idea, so we must calculate a different reference vector.
Avoid Obstacle Behavior
Going towards the goal when there’s an obstacle in that direction is a case in point. Instead of running headlong into things in our way, let’s find a way to avoid them.
To simplify the question, let’s now forget the goal point completely and just make the following our objective:When there are no obstacles in front of us, move forward. When an obstacle is encountered, turn away from it until it is no longer in front of us.
Accordingly, when there is no obstacle in front of us, we want our reference vector to simply point forward. Then ω will be zero and v will be maximum speed. However, as soon as we detect an obstacle with our proximity sensors, we want the reference vector to point in whatever direction is away from the obstacle. This will cause ω to shoot up to turn us away from the obstacle, and cause v to drop to make sure we don’t accidentally run into the obstacle in the process.
A neat way to generate our desired reference vector is by turning our nine proximity readings into vectors, and taking a weighted sum. When there are no obstacles detected, the vectors will sum symmetrically, resulting in a reference vector that points straight ahead as desired. But if a sensor on, say, the right side picks up an obstacle, it will contribute a smaller vector to the sum, and the result will be a reference vector that is shifted towards the left.

Here is the code that does this in avoid_obstacles_controller.py:
# sensor gains (weights)
self.sensor_gains = [ 1.0+( (0.4*abs(p.theta)) / pi )
for p in supervisor.proximity_sensor_placements() ]
...
# return an obstacle avoidance vector in the robot's reference frame
# also returns vectors to detected obstacles in the robot's reference frame
def calculate_ao_heading_vector( self ):
# initialize vector
obstacle_vectors = [ [ 0.0, 0.0 ] ] * len( self.proximity_sensor_placements )
ao_heading_vector = [ 0.0, 0.0 ]
# get the distances indicated by the robot's sensor readings
sensor_distances = self.supervisor.proximity_sensor_distances()
# calculate the position of detected obstacles and find an avoidance vector
robot_pos, robot_theta = self.supervisor.estimated_pose().vector_unpack()
for i in range( len( sensor_distances ) ):
# calculate the position of the obstacle
sensor_pos, sensor_theta = self.proximity_sensor_placements[i].vector_unpack()
vector = [ sensor_distances[i], 0.0 ]
vector = linalg.rotate_and_translate_vector( vector, sensor_theta, sensor_pos )
obstacle_vectors[i] = vector # store the obstacle vectors in the robot's reference frame
# accumluate the heading vector within the robot's reference frame
ao_heading_vector = linalg.add( ao_heading_vector,
linalg.scale( vector, self.sensor_gains[i] ) )
return ao_heading_vector, obstacle_vectors
Using the resulting ao_heading_vector as our reference for the robot to try to match, here are the results of running the robot using only the Avoid-Obstacles controller, ignoring the goal point completely. The robot bounces around aimlessly, but it never collides with an obstacle, and even manages to navigate some very tight spaces:

Hybrid Automata – Behavior State Machine
So far we’ve described two behaviors – Go-to-Goal and Avoid-Obstacles – in isolation. Both perform their function admirably, but in order to successfully reach the goal in an environment full of obstacles, we need to combine both of them together.
The solution we will use lies in a class of machines that has the supremely cool-sounding designation of hybrid automata. A hybrid automaton is programmed with several different behaviors, or modes, as well as a supervising state machine that switches between these behaviors depending on conditions.
Equipped with our two handy behaviors, a simple logic suggests itself: When there is no obstacle detected, use the Go-to-Goal behavior. When an obstacle is detected, switch to Avoid-Obstacles behavior until the obstacle is no longer detected.
As it turns out, however, this logic will produce a lot of problems. What this system will tend to do when it encounters an obstacle is to turn away from it, then as soon as it has moved away from it, turn right back around and run into it again. The result is an endless loop of rapid switching that renders the robot useless. In the worst case, the robot may switch between behaviors with every iteration of the control loop – a state known as a Zeno condition.
What we need, therefore, is one more behavior, which is specialized with the task of getting around an obstacle and reaching the other side.
Follow Wall Behavior
Here’s the idea: when we encounter an obstacle, take the two sensor readings that are closest to the obstacle and use them to estimate the surface of the obstacle. Then, simply set our reference vector to be parallel to this surface. Keep following this wall until A) the obstacle is no longer between us and the goal, and B) we are closer to the goal than we were when we started. Then we can be certain we have navigated the obstacle properly.
With our limited information, we can’t say for certain whether it will be faster to go around the obstacle to the left or to the right. To make up our minds, we select the direction that will move us closer to the goal immediately. To figure out which way that is, we need to know the reference vectors of the Go-to-Goal behavior, the Avoid-Obstacle behavior, as well as both of the possible Follow-Wall reference vectors. Here is an illustration of how the final decision is made (in this case, the robot will choose to go left):

Determining the Follow-Wall reference vectors turns out to be a bit more involved than either the Avoid-Obstacle or Go-to-Goal reference vectors. Take a look at follow_wall_controller.py to see how it’s done.
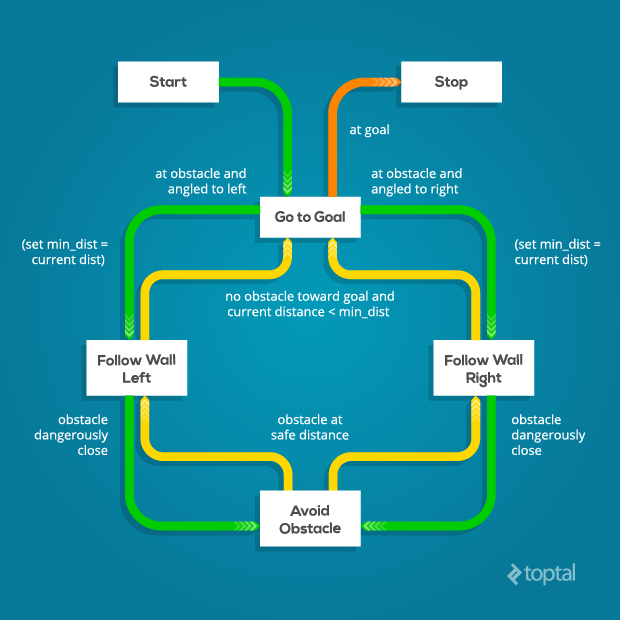
Final Control Design
The final control design uses the Follow-Wall behavior for almost all encounters with obstacles. However, if the robot finds itself in a tight spot, dangerously close to a collision, it will switch to pure Avoid-Obstacles mode until it is a safer distance away, and then return to Follow-Wall. Once obstacles have been successfully negotiated, the robot switches to Go-to-Goal. Here is the final state diagram, which is implemented by supervisor_state_machine.py:
Here is the robot successfully navigating a crowded environment using this control scheme:

Tweak, Tweak, Tweak – Trial and Error
The control scheme that comes with Sobot Rimulator is very finely tuned. It took many hours of tweaking one little variable here, and another equation there, to get it to work in a way I was satisfied with. Robotics programming often involves a great deal of plain old trial-and-error. Robots are very complex and there are few shortcuts to getting them to behave optimally in a robot simulator environment.
Robotics often involves a great deal of plain old trial-and-error.
I encourage you to play with the control variables in Sobot Rimulator and observe and attempt to interpret the results. Changes to the following all have profound effects on the simulated robot’s behavior:
- the error gain
kPin each controller - the sensor gains used by the Avoid-Obstacles controller
- the calculation of v as a function of ω in each controller
- the obstacle standoff distance used by the Follow-Wall controller
- the switching conditions used by
supervisor_state_machine.py - pretty much anything else
When Robots Fail
We’ve done a lot of work to get to this point, and this robot seems pretty clever. Yet, if you run Sobot Rimulator through several randomized maps, it won’t be long before you find one that this robot can’t deal with. Sometimes it drives itself directly into tight corners and collides. Sometimes it just oscillates back and forth endlessly on the wrong side of an obstacle. Occasionally it is legitimately imprisoned with no possible path to the goal. After all of our testing and tweaking, sometimes we must come to the conclusion that the model we are working with just isn’t up to the job, and we have to change the design or add functionality.
In the robot universe, our little robot’s “brain” is on the simpler end of the spectrum. Many of the failure cases it encounters could be overcome by adding some more advanced AI to the mix. More advanced robots make use of techniques such as mapping, to remember where it’s been and avoid trying the same things over and over, heuristics, to generate acceptable decisions when there is no perfect decision to be found, and machine learning, to more perfectly tune the various control parameters governing the robot’s behavior.
Conclusion
Robots are already doing so much for us, and they are only going to be doing more in the future. While robotics programming is a tough field of study requiring great patience, it is also a fascinating and immensely rewarding one. I hope you will consider getting involved in the shaping of things to come!
Acknowledgement: I would like to thank Dr. Magnus Egerstedt and Jean-Pierre de la Croix of the Georgia Institute of Technology for teaching me all this stuff, and for their enthusiasm for my work on Sobot Rimulator.
About the author
Nicholas is a professional software engineer with a passion for quality craftsmanship. He loves architecting and writing top-notch code, and is proud of his ability to synthesize and communicate ideas effectively to technical and non-technical folks alike. Nicholas always enjoys a novel challenge.